Boa tarde pessoal a um bom tempo trabalho em uma classe de manipulação de matrizes, até o momento só implemente a cópia de matrizes e o operador Igual (=) e a multiplicação (*),
Na classe a métodos que cria matrizes em torno do eixo X, Y e Z, na Engine o Z aponta para cima no caso para setar a posição da câmera fica desta maneira
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
Matrix rz,ry,rx,mm;
rz.RotZ(90);
ry.RotY(90);
rx.RotY(-68);
glLoadIdentity();
Matrix rz,ry,rx,mm;
rz.RotZ(90);
ry.RotY(90);
rx.RotY(-68);
mm.setIdentity();
mm = ry * rz *rx;
glMultMatrixf(mm.m);
mm = ry * rz *rx;
glMultMatrixf(mm.m);
glTranslatef(6.78,18.78,-5);
O Resultado é este:
Segue abaixo as classes de Matrizes
//Matrix.h
# include "vec3d.h"
class Matrix
{
public:
float m[16];
Matrix();
void setIdentity();
void RotX(float a);
void RotY(float a);
void RotZ(float a);
Matrix& operator*(const Matrix& mat);
Matrix& operator=(const Matrix& mat);
//Matrix operator+(Matrix& mat);
//Matrix operator-(Matrix& mat);
};
//Matrix.cpp
#include
#define M(x,y) (y*4+x)
/**
* Classe para Manipulação de matrizes
*/
Matrix::Matrix()
{
setIdentity();
}
/**
* seta a matrix como identidade
* |1 0 0 0|
* |0 1 0 0|
* |0 0 1 0|
* |0 0 0 1|
*/
void Matrix::setIdentity()
{
m[0] = 1.0f; m[1] = 0.0f; m[2] = 0.0f; m[3] = 0.0f;
m[4] = 0.0f; m[5] = 1.0f; m[6] = 0.0f; m[7] = 0.0f;
m[8] = 0.0f; m[9] = 0.0f; m[10] = 1.0f; m[11] = 0.0f;
m[12] = 0.0f; m[13] = 0.0f; m[14] = 0.0f; m[15] = 1.0f;
}
/**
* Multiplica a Matrix por um vetor 3x1
*/
vec3d vecbymat(vec3d vec, Matrix mat)
{
vec3d r;
r.x = mat.m[0] * vec.x + mat.m[1] * vec.y + mat.m[2] * vec.z + mat.m[3];
r.y = mat.m[4] * vec.x + mat.m[5] * vec.y + mat.m[6] * vec.z + mat.m[7];
r.z = mat.m[8] * vec.x + mat.m[9] * vec.y + mat.m[10] * vec.z + mat.m[11];
return r;
}
Matrix& Matrix::operator*(const Matrix& mat)
{
float _m[16];
for(int i = 0; i <4;i++)
for(int j = 0; j<4; j++)
{
float sum = 0.0f;
for(int k=0;k<4;k++)
sum += this->m[i*4+k] * mat.m[k*4+j];
_m[i*4+j] = sum;
}
memcpy(this->m,_m,sizeof(float)*16);
return *this;
}
Matrix& Matrix::operator=(const Matrix& mat)
{
memcpy(this->m,mat.m,sizeof(float)*16);
return *this;
}
void Matrix::RotX(float a)
{
float c = cosf(DEG2RAD(a));
float s = sinf(DEG2RAD(a));
m[0] = 1.0f; m[1] = 0.0f; m[2] = 0.0f; m[3] = 0.0f;
m[4] = 0.0f; m[5] = c; m[6] = s; m[7] = 0.0f;
m[8] = 0.0f; m[9] = -s; m[10] = c; m[11] = 0.0f;
m[12] = 0.0f; m[13] = 0.0f; m[14] = 0.0f; m[15] = 1.0f;
}
void Matrix::RotY(float a)
{
float c = cosf(DEG2RAD(a));
float s = sinf(DEG2RAD(a));
m[0] = c; m[1] = 0.0f; m[2] = -s; m[3] = 0.0f;
m[4] = 0.0f; m[5] = 1.0f; m[6] = 0.0f; m[7] = 0.0f;
m[8] = s; m[9] = 0.0f; m[10] = c; m[11] = 0.0f;
m[12] = 0.0f; m[13] = 0.0f; m[14] = 0.0f; m[15] = 1.0f;
}
void Matrix::RotZ(float a)
{
float c = cosf(DEG2RAD(a));
float s = sinf(DEG2RAD(a));
m[0] = c; m[1] = s; m[2] = 0.0f; m[3] = 0.0f;
m[4] = -s; m[5] = c; m[6] = 0.0f; m[7] = 0.0f;
m[8] = 0.0f; m[9] = 0.0f; m[10] = 1.0f; m[11] = 0.0f;
m[12] = 0.0f; m[13] = 0.0f; m[14] = 0.0f; m[15] = 1.0f;
}
Só para refrescar a memória as matrizes de rotação seguem abaixo:

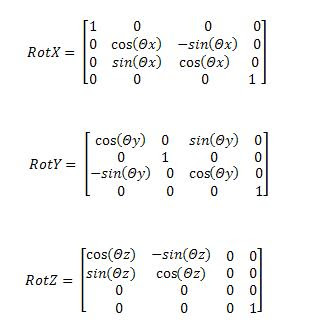
Sem comentários:
Enviar um comentário